交互作用項/Interaction term
交互作用項の結果の解釈
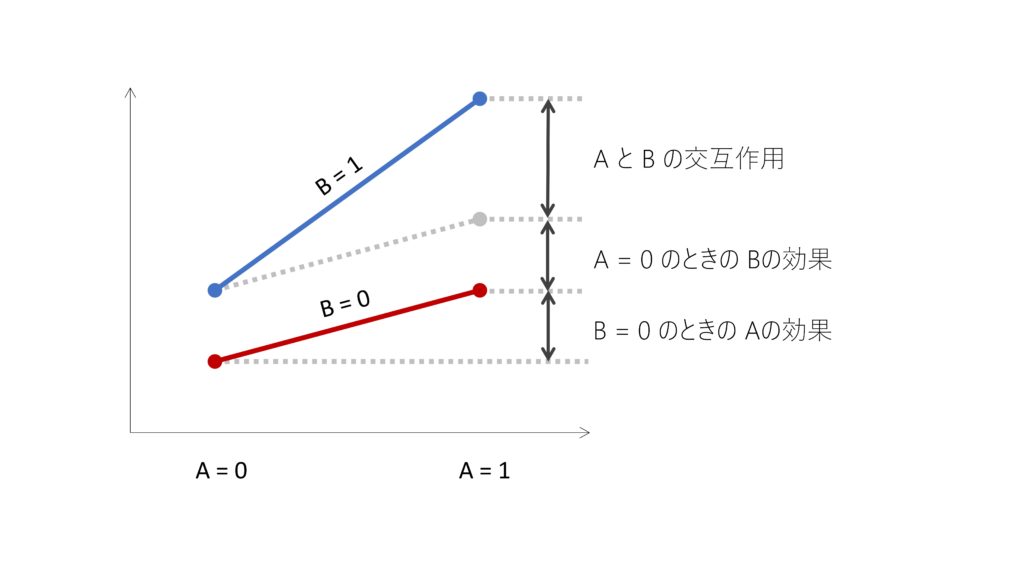
AとBの交互作用項を入れたときの主効果の意味は、
・主効果 A : B = 0 の時の A の効果
・主効果 B : A = 0 の時の B の効果
です。「交互作用項を入れたときの主効果には意味がない!」などという人がいますが、意味がないことはありません。
もっとも意味がないと言いたくなる人の気持ちも、場合によってはわかります。例えば年齢と喫煙の交互作用項をモデルに入れる場合、年齢の主効果は喫煙=0の時の効果、喫煙の主効果は年齢=0の時の効果になります。0歳の時の喫煙の効果を調べることに意味があるかと言えば、0歳で喫煙している人はいないでしょうから、「意味はありません」。ただ、それが何にも意味がないかと言われれば、今言ったような内容が結果の解釈となるわけです。1逆に、解釈する意味のある値にしたいのであれば、平均年齢が0になるように変数を変換するなどの方法が考えられます。
Stataのスクリプト
Stataで交互作用項を入れる場合には「♯」を使います。結果変数がyでAとBの相互作用を見たいときは、
のいずれかが一般的でしょう。「i.」はその変数が離散変数20/1とか。Categorical variableという。であることを宣言する接頭辞です。上記二つの方法に加えて、AとBの交互作用項を事前に作るという方法もあります。
交互作用を検討する変数が連続変数である場合には、「c.」を変数名の前につけましょう。
上記例だと一つ目が離散変数Aと連続変数Cの交互作用、二つ目は連続変数Cと連続変数Dの交互作用になります。
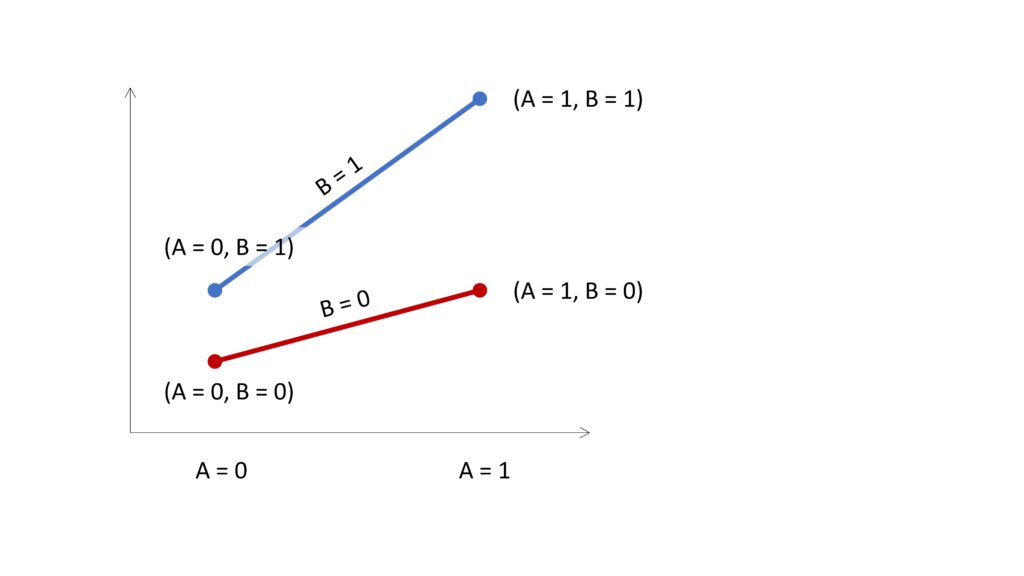
ちなみに、離散変数どうしの交互作用項を見るときに、♯ひとつだけをつかうと、交互作用を検討している変数が取りうる値の組み合わせごとの推定値を返します。Aの取りうる値が0か1、Bの取りうる値も0か1である場合を具体的に書くと、
下図で示すように、A=0, B= 0をreferenceとした場合の、A=0, B=1、A=1, B=0、A=1, B=1、それぞれの場合の値を算出します。得られた3点の点推定値と信頼区間はA=0, B=0というreference groupと比較した場合の数値です。それらの値単独では交互作用があったかどうかは分かりませんが、それぞれの組み合わせの場合にどのような値を取ることになるのか確認するという意味では便利です。
具体例①:血圧に関する年齢と性別の交互作用
変数名
・bp_after: 血圧(連続値)
・agegrp:1:30-45;2:46-59;3:60+
・sex:0:男性;1:女性
| 1行目: | データの読み込み。 |
| 2~4行目: | 結果の説明をしやすいように年齢階級を減らしました。 |
| 5、6行目: | II・III度高血圧を収縮期血圧のみで定義しました。3かなり雑な定義です。 |
| 7行目: | ♯ひとつをつかって交互作用を定義した場合です。ロジスティック回帰分析にしています。4本当はLogistic regressionのRare disease assumptionが満たされていないので、Poisson with a robust variance estimatorなどが望ましいです。 |
| 8行目: | ♯ふたつをつかって交互作用を定義した場合です。 |
| 9行目: | 交互作用の様子をグラフにするためのコマンド marginを使用しています。sexが0と1、agegrpが1と3の場合に取りうる組み合わせごとに予測値を計算しろという指令です。6行目の後にやっても、5行目の後にやっても同じ結果を返します。 |
| 10、11行目: | marginで計算した値をグラフにするコマンドです。 |
7行目の結果:
男性で年齢が若い群をReference groupにしたときに、男性で高齢群、女性で若い群、女性で高齢群それぞれにおいて、血圧が160 mmHg以上になるオッズ比を計算しています。
Logistic regression Number of obs = 120
LR chi2(3) = 26.40
Prob > chi2 = 0.0000
Log likelihood = -58.33007 Pseudo R2 = 0.1845
------------------------------------------------------------------------------
ht | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
sex#age2 |
Male#1 | 3.857143 2.228282 2.34 0.019 1.243152 11.9676
Female#0 | .1093117 .0874682 -2.77 0.006 .0227803 .5245354
Female#1 | .8901099 .52814 -0.20 0.844 .2782208 2.847723
|
_cons | .4814815 .1625384 -2.17 0.030 .2484455 .9330996
------------------------------------------------------------------------------
8行目の結果:
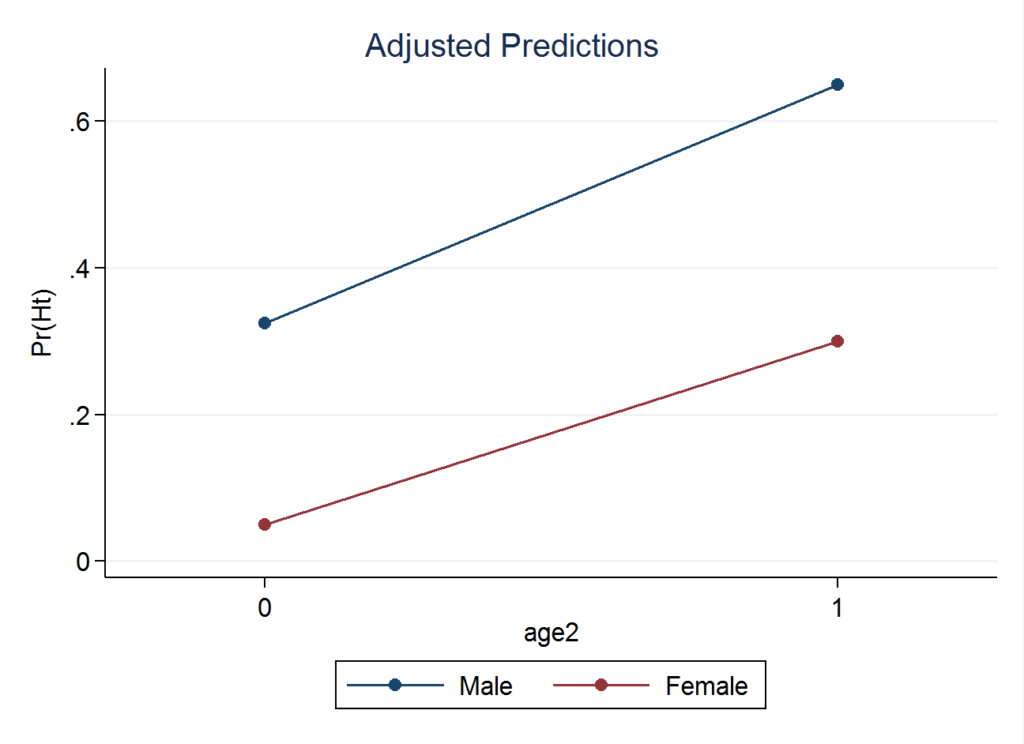
sex#agegrpが有意ではないので、交互作用があるとは言えないという結論になります。
Logistic regression Number of obs = 120
LR chi2(3) = 26.40
Prob > chi2 = 0.0000
Log likelihood = -58.33007 Pseudo R2 = 0.1845
------------------------------------------------------------------------------
ht | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
sex |
Female | .1093117 .0874682 -2.77 0.006 .0227803 .5245354
1.age2 | 3.857143 2.228282 2.34 0.019 1.243152 11.9676
|
sex#age2 |
Female#1 | 2.111111 2.212291 0.71 0.476 .270716 16.46298
|
_cons | .4814815 .1625384 -2.17 0.030 .2484455 .9330996
------------------------------------------------------------------------------
これを図にするとこうなります。
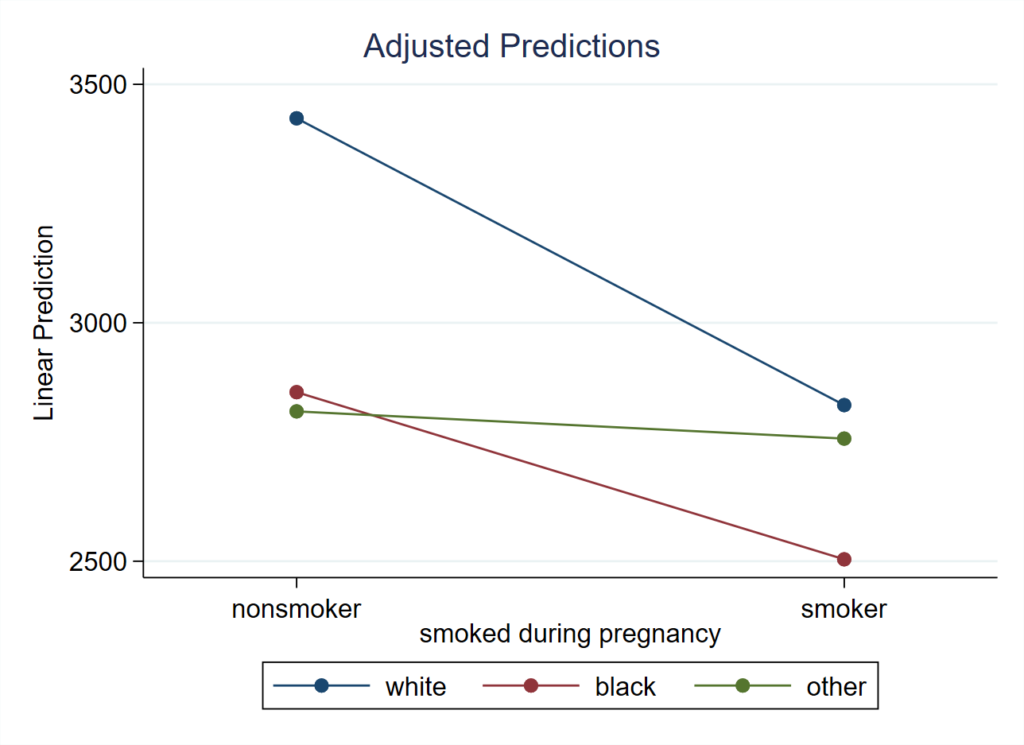
具体例②:出生体重の決定要因
変数名
・bwt:出生体重
・race:1:白人;2:黒人;3:その他
・smoke:0:喫煙なし;1:喫煙あり
Source | SS df MS Number of obs = 189
-------------+---------------------------------- F(5, 183) = 6.19
Model | 14455540.4 5 2891108.08 Prob > F = 0.0000
Residual | 85459758.2 183 466993.214 R-squared = 0.1447
-------------+---------------------------------- Adj R-squared = 0.1213
Total | 99915298.6 188 531464.354 Root MSE = 683.37
-------------------------------------------------------------------------------
bwt | Coef. Std. Err. t P>|t| [95% Conf. Interval]
--------------+----------------------------------------------------------------
race |
black | -574.25 199.5008 -2.88 0.004 -967.8674 -180.6326
other | -614.5136 138.2182 -4.45 0.000 -887.2198 -341.8075
|
smoke |
smoker | -601.3654 139.979 -4.30 0.000 -877.5456 -325.1851
|
race#smoke |
black#smoker | 250.8654 308.9992 0.81 0.418 -358.7938 860.5245
other#smoker | 544.2957 258.8455 2.10 0.037 33.59038 1055.001
|
_cons | 3428.75 103.0218 33.28 0.000 3225.487 3632.013
-------------------------------------------------------------------------------
Multiplicative interaction vs. Additive interaction
交互作用にはMultiplicative interactionとAdditive interactionがあります。♯で普通に交互作用を定義するときに得られるのは、ロジスティック回帰やポワソン回帰を使っている場合はMultiplicative interaction(具体例①)、線形回帰を使用している場合はAdditive interaction(具体例②)になります。これらを交互作用の結果として示すことが一般的なのですが、例①の場合にAdditive interactionを計算することもできます。
なぜロジスティック回帰やポワソン回帰の場合でもAdditive interactionを計算するのかという理由について深く知りたい人は、以下のリンクを参考にするといいと思います。
・コロ助氏のブログ 「交互作用」とはなにか ([Link])
・VanderWeele, T. J., & Knol, M. J. (2014). A tutorial on interaction. Epidemiologic Methods, 3(1), 33-72. [Link]
ここでは、例①の場合にAdditive interactionをどのように計算するか示しておくだけにします。交互作用項を別途新規の変数として定義する必要があります。
------------------------------------------------------------------------------
ht | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_nl_1 | .4308714 .6482181 0.66 0.506 -.8396128 1.701356
------------------------------------------------------------------------------この結果からいえることは、例①の場合は、Additive scaleでもMultiplicative scaleでも交互作用があるとは言えないということです。

your authored material stylish. nonetheless